How many equations?

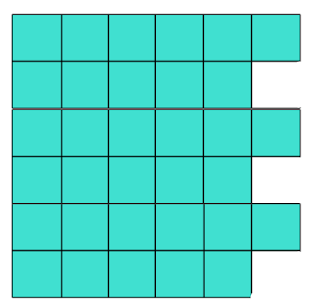
I saw this image recently on Twitter with the question: How many ways can your find to make 7/7? Students can use pattern blocks to represent fractions, and then write number sentences and draw a representation to match their blocks.  This could be a great exploration for beginning fraction concepts. It could be made with different wholes depending on your grade level.

It could also be asked as "How many ways can you find to make 7/6?...

What question might you ask to go with this pattern?  Goals in our classrooms should include making the math visual, allowing for all students to be able to access the math, and to provide rigor for our students.

Open-ended problems like this provide all of these things for our students, and are relatively easy for us to embed into our instruction through workshop.  The problems above are fraction problems, but couldn't primary students do the same with 5 or 13 cubes?  How many ways can they find to make 5?  Is that all of the ways?  Can they prove it?

Putting our students into situations where they get to work with manipulatives and make sense of numbers is an important part of their learning.  Can you think of ways that students in your classroom can explore number, whether it is whole numbers, fractions, decimals or something else?  How many equations can they make, and can they be sure that they have found them all?

Multiplying by 11 Exploration

Multiplying by 11 has an evident pattern for our beginning multipliers.  They love the fact that they know how to multiply by a number larger than 10! We need to be sure that they are building a conceptual understanding of what 11 times another number looks like.

In addition, we want to give our students an opportunity to identify patterns.  Why does 11 times a number less than 10 ten give a double digit number of the other factor? Help them use visual pieces to make sense of it.  I think these 10 frames +1 make it easy to see, but maybe they have another idea.

Once they can identify why 11 x 3 = 33, take them on another exploration.

Can they find the pattern when you take 11 x a 2 digit number?  Can they figure out why it happens?

11 x 12 = 132

15 x 11=165

When multiplying 11 by a 2-digit number, the tens digit is the same as the hundreds digit in the product and the ones digit in the product is the same as the ones digit in the 2-digit factor.  The tens digit in the product is the sum of the hundreds and ones digit.

Don't tell your students this pattern.  Give them the tools to uncover it, and then let them use the visuals to see if they can find an explanation.  Many 4th and 5th graders should be able to explain.    What happens when the digits in the 2 digit number have a sum greater than 10?  Looking at the groups of 11 can they figure out what is happening?
Will this pattern continue into 3 digit numbers?  What stays the same? What changes?

This is not to be taught or used as "a trick." This exploration is to help students find patterns in numbers and place value and for them to be able to see why it is happening. It is important that we give them lots of opportunities to explore and make sense of the things that they find.

Growth Mindset Resources

from the great Jo Boaler and Youcubed!

Are you looking to strengthen your capabilities when teaching students about Growth Mindset?  Jo Boaler has created  this resource to help us grow as educators so that we can help our students grow as learners!

The site focuses on 5 Mathematical Mindsets and gives us clear pictures of what they should like in the classroom.  There are even videos that we can watch to help us understand. She has a user guide and a teacher's guide to help us understand where we are going.

This summer, take the time to explore this fabulous resource so that you can learn even more about growth mindset in our classroom.  I don't think you'll be sorry!

Unit fraction computation exploration

What is 1/2 - 1/3?
How about 1/2 * 1/3?

What is 1/5 - 1/6?
How about 1/5 * 1/6?

What pattern do you see in the fractions above? 

Will this work for all unit fractions?  Why?  

Are there other fractions it will work for? 

Is there a pattern when you increase the common numerator? (i.e. 2/7-2/8?)

4 Triangles Exploration

This exploration comes from Marilyn Burns, and it goes very nicely with her book, The Greedy Triangle.  

In this exploration, small groups work together to see how many polygons they can make with four triangles. The trick is:  the construction of the polygons must follow a specific rule.

To get started, put your students in pairs or groups of three.  The students will need a large paper on which to place their findings. Students must use all four triangles to create their polygons.  The easiest way is to use post it notes and cut them diagonally to form congruent triangles.  You might want to give them two different colors of post it notes so that each polygon they form has two triangles of two different colors.  (The colors just help to make the lines between the triangles more distinguishable.)

As far as the rules, you might want to show them some that don't follow the rules and some that do and see if they can figure out the rules.   

 These two do not follow the rule.

This one follows the rule.

Here is the rule that their 4-triangles must follow:

Sides that touch must be the same length and match up exactly

As students make polygons that match this rule, have them tape onto their paper.  The goal is for them to find as many polygons as they can.  (There are 14).  

Be sure to build in time to have a discussion about what shapes were formed.  Consider taking the time to sort them and have the students decide what rule you used to sort them.  This end of exploration discussion is key to the students making sense of the exploration by talking about it, and it gives you more time to infuse more vocabulary into the lesson!

What do they think would happen if you gave them five triangles?  How would that change the number of polygons?

Possible ways to sort:  number of sides, types of angles, lines of symmetry, convex/concave, perimeter... Do your students know why you can't sort them by area?

Give this exploration a try and let me know what you think--better yet: What your students think!!

Summertime Ideas

As summer approaches, we need to remember that this important time of rejuvenation offers students time to explore, play, and be a kid.  It is not about daily academic programs or workbooks to complete.  

It is good for parents to continue to offer their child ways to maintain academic skills while also helping them to enjoy the summer. Besides the list of ideas I have shared before, parents may want to consider using Bedtime Math. It offers short interesting math practice that parents and children talk through and discuss together.  The discussion is the important part of this app; not the answer.  It allows parents to engage children with math in a non-threatening, fun way. Another good site that is geared towards parents is called Table-talk math. The site is in conjunction with a book of the same name by John Stevens, but this site offers ideas and examples of concepts for parents to talk with their children about.

Consider sharing these sites or the list of the ideas from my earlier blog post with parents.  As a parent, I know I always appreciate when teachers give me ideas of things that I can do to enrich my children.  I'm sure yours will, too!

Primary Exploration of Multiples

Time for our students to explore number concepts is important!  It allows our students to play with numbers in a non-threatening way and to make sense of the math in a way that works for them. This primary exploration allows students to play with numbers in a cooperative way.

Partner your students up.  Each has a different color of unifix cubes.  One is responsible for the sticks of 2, and the other for sticks of 3.  

 After they have created their "sticks," they begin to hook their colors together to see if they can get them to match up.  In this case 3 + 3 = 6 and 2 + 2 + 2 = 6.

 Have them continue in this way, finding how many times the two groups will match up.  Encourage them to write number sentences to match their blocks.  3 + 3 + 3 + 3 = 2 + 2 + 2 + 2 + 2 + 2

Can they begin to see the pattern on when the blocks match up?  When they run out of blocks, can they figure out how many they would need to make the next match? You might take this opportunity to introduce the word multiples in 2nd or 3rd grade.  You could differentiate/extend this as you wish for your students by changing the lengths of the sticks...

When you are done with the exploration, be sure to have a Notice and Wonder session.  Write down the things that your students find so that you can refer to it at later times. 

What other ideas do you have for this activity or one similar to it?